
Science in Hinduism-Large numbers and infinity
In my previous article, we saw how Indian scholars laid out the foundation of modern mathematics. However, in my previous article, we saw about only the basic number system. In this article, we will go one step forward to see the concept of large numbers in ancient Indian literature including Vedic texts.
In all early civilizations, the first expression of mathematical understanding appears in the form of counting systems. Numbers in early civilization were typically done using symbols or series of lines separated by space. However, lots of difficulties were faced by the western concept of number system. Let us analyze their difficulties
Difficulties in Number system of western world
In the Western world, large numbers were not in use until quite recently with the advent of modern science in the nineteenth century. In ancient times, Greeks number system were based on myriad (i.e 10,000) and their largest was a myriad myriad, i.e 100,000,000
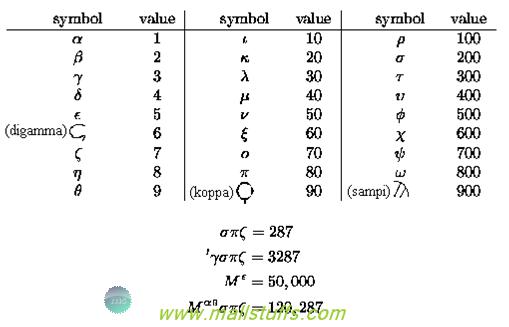
Greek Number system
Later, Archimedes (287-212 BC) devised a system of large numbers up to , by using powers of a myriad myriad. However, Archimedes proposed his numbering system based on power of myriad and hence, would have faced notational difficulties in devising numbers system based on power of myriad. So, he stopped at this number because of not being able to derive any new ordinal numbers larger than 'myriad myriadth'.
, by using powers of a myriad myriad. However, Archimedes proposed his numbering system based on power of myriad and hence, would have faced notational difficulties in devising numbers system based on power of myriad. So, he stopped at this number because of not being able to derive any new ordinal numbers larger than 'myriad myriadth'.
Shortly, after Archimedes devised a system based on power of 10, Appollonious of perga devised a more practical number system which were not based on power of 10 but on naming power of a myriad, for example,
 Would be a myriad squared.
Would be a myriad squared.
Why there was a Need of a better number system
Using myriad, western scholars were not able to derive all possible large numbers. Hence, western scholars were facing difficulties in representing or deriving many mathematical concepts. Hence, there was a rising need of a better, More concise, more consistent and more precise number system. This is where the need of adopting the Indian number system came into place. Actually, when the westerners were thinking in ones or two, Indians had invented the whole place value system with numbers extending up to power of 621. In fact, by the 7th century BCE, Indian scholars reintroduced the notion of infinity as the quantity whose denominator is zero.
There was no concept of infinity in western world and only by the end of 13th century, Roman scholars introduced the concept of representing large numbers as millions i.e. 1,000,000 was expressed as decies centena milia, (ten hundred thousand); which was evidently called as million.
Let us now see how the Indians have dominated the number system
Number System in Ramayana
It may be surprising to know that Indian sages used large numbers up to power of 1062 and that too millions of years ago with the first to use it were Sage Valmiki (Author of Ramayana)
Following verse from Ramayana said to be written at least 12 million years ago in Tretâyuga, presents a number system up to power of 1062, big enough to be represent infinity.
Verse:
�atam �atasahsrânam, kotim âhurmanisinah
Œatam kotisahasrânam �ankurityabhidhiyate
Above verse can be precisely translated as
Œatam œatasahsram = One Koti
ie. Hundred hundred thousand = 100, 00,000 = 1 crore = 107
Œatam Kotisahsram = One Œanku
ie. Hundred thousand crore = 100, 000, 0000,000
= Œanku = 1012
1 Koti = 107 = 1 crore
1 Œanku = 1012 = 1 lakh crore
1 Mahaœanku = 1017
1 Vrndam = 1022
1 Mahavrndam = 1027
1 Padmam = 1032
1 Mahapadmam = 1037
1 Kharvam = 1042
1 Mahakharvam = 1047
1 Samudram = 1052
1 Ougham = 1057
1 Mahaugham = 1062
This number is actually the count of the monkey soldiers who built the historic Ram Sethu (Also known as Adam Bridge).

Monkey soldiers Building Ram sethu
While inhabitants of other continents were using stones and fingers to count, Vedic sages counted in trillions & trillions to measure the cosmic concepts of this universe.
Number system in Vedas:
Many Vedic texts points to the decimal number system. Yajurveda describes the number system with place value up to 18 places, the highest called as parardha.
For Example, after preparing bricks for a Vedic ritual, Rishi(Sage) Medhâtithi prays to the Lord of fire, Agni
Verse:
Imâ me Agna istakâ dhenava
Santvekâ ãa desa ãa satam ãa
Sahasram ćāyutam ãa niyutam ãa
Prayutam ćārbudam ãa nyarbudam ãa
Samudrasãa madhyam ćāntasãa
Parârdhasãaita me agna ishtakâ
Dhenavasantvamutrâmushmimlloke .
Translation:
Oh Agni! Let these bricks be milk giving cows to me
Please give me one and ten and hundred and thousand
Ten thousand and lakh and ten lakh and
One crore and ten crore and hundred crore,
A thousand crore and one lakh crore in this world and other worlds too.
eka - 1 - one - 10�
dasa - 10 - ten - 101
satam - 100 - hundred - 102
sahasram - 1000 - thousand - 103
ayutam - 10000 - ten thousand - 104
niyutam - 100000 - one lakh - 105
prayutam -1000000 - ten lakh - 106 - million
arbudam -10000000 - one crore - 107 - ten million
nyarbudam -100000000 - ten crore - 108 - hundred million
samudram -1000000000 - hundred crore- 109 - billion
madhyam -1000000000 - thousand crore- 1010 - ten billion
antam -100000000000 - ten thousand crore-1011 - hundred billion
parardham -1000000000000- one lakh crore - 1012 - trillion
Even the concept of Fibonacci number can be found in Vedic verse translated as
The sun flower smiles at you with 34, 55 florets. (34, 55 are the numbers in the sequence of Fibonacci number.)

Sacred text of vedas
Concept of Infinity in vedas
Concept of infinity was used repeatedly in Vedic era. Latest being the vishwa roop darshan of lord Krishna where lord Krishna is shown as ananta, meaning “infinity” or “having no end”. Some of the other words used in vedic texts are purnam, asamkhyata and aditi. For Ex:Word Asamkhyata is used in Yajur Veda and Brihadaranyaka Upanishad to represent the number of mysteries of Indra as ananta. Following verse from yajurveda describes the mathematical concept of infinity. However, this verse (Shloka) is more metaphysical than matahemical
Verse:
pûrnamadah p ûrnamidam pûrnât pûrnamudacyate
p ûrnâsya pûrnamadaya p ûrnamevâvasishyate
Translation:
From infinity is born infinity.
When infinity is taken out of infinity, left over is only infinity.
Another Vedic verse with concept of infinity is
Om purnam adah purnam idam
Purnat purnam udacyate
Purnasya purnam adaya
Purnam evâva�is�yate
Translation
OM- the Complete Whole; purnam- perfectly complete; adah-that; purnam-perfectly complete; idam- this phenomenal world; purnat-the all-perfect; purnam-complete unit; udacyate- is produced; purnasya- Complete Whole; purnam- completely; adaya- having been taken away; purnam-the complete; eva- even; avasisyate-is remaining.
Atharveda has some verses signifying the concept of one, arithmetic progression, and arithmetic series. Below are the numbers along with the term used in Vedas and other ancient Indian texts
Numerals greater then 100
| Number | Sanskrit | |
|
200 | Dvisata |
|
300 | Trisata |
|
356 | sat pancasat trisata |
|
400 | Catursata |
|
500 | Pancasata |
|
1000 | Sahasra |
|
2000 | Dvisahasra |
|
3000 | Trisahasra |
|
4000 | Catursahasra |
|
10,000 | dasasahasra, ayuta |
|
20,000 | Vimsatsahasra |
|
30,000 | Trimsatsahasra |
|
100,000 | satasahasra, laksha, lak |
|
200,000 | dvi-sata-sahasra |
|
300,000 | tri-sata-sahasra |
|
1,000,000 | prayuta, niyuta |
|
10,000,000 | koti, krore |
|
100,000,000 | arbuda, vrnda, nyarbuda |
Numerals from Billion and above
| Number | Sanskrit | |
|
1,000,000,000 | abja, shatakoti, maharbuda, nikharva, nikarvaka, badva |
|
10,000,000,000 | Kharva |
|
100,000,000,000 | nikharva, akshita |
|
1,000,000,000,000 | mahaapadma, antya, antyam, nikharva |
|
10,000,000,000,000 | sha.nku |
|
100,000,000,000,000 | Jaladhi |
|
1000,000,000,000,000 | Antya |
|
10,000,000,000,000,000 | Madhya |
|
100,000,000,000,000,000 | Paraardha |
Word-Numeral Decimal System
Indian scholars expressed all large numbers using the decimal number system. The highest power of 10 named today is 1030 (Deca). But ancient Indian mathematicians had exact names for powers up to 1053.
| Word-Numeral | Decimal Equivalent | |
|
Ekam | 100 |
|
Dashkam | 101 |
|
1 Shatam | 102 |
|
1 Shahashram | 103 |
|
10 Dash Shahashram | 104 |
|
Laksha | 105 |
|
Dash Laksha | 106 |
|
Kotihi | 107 |
|
Ayutam | 109 |
|
Niyutam | 1011 |
|
Kankaram | 1013 |
|
pakoti | 1014 |
|
Vivaram | 1016 |
|
Pararadahaa | 1017 |
|
kshobhya | 1018 |
|
Nivahata or vivaha | 1019 |
|
Utsangaha or kotippakoti | 1021 |
|
Bahulam | 1023 |
|
Naagbaalaha | 1025 |
|
Titlambam | 1027 |
|
nahuta | 1028 |
|
Vyavasthaanapragnaptihi or titlambha | 1029 |
|
Hetuhellam or vyavasthanapajnapati | 1031 |
|
Karahuhu | 1033 |
|
Hetvindreeyam or ninnahuta | 1035 |
|
Sampaata Lambhaha or hetvindriya | 1037 |
|
Gananaagatihi or samaptalambha | 1039 |
|
Niravadyam or gananagati | 1041 |
|
akkhobini | 1042 |
|
Mudraabalam or niravadya | 1043 |
|
Saraabalam | 1045 |
|
Vishamagnagatihi | 1047 |
|
Sarvagnaha or bindu | 1049 |
|
Vibhutangaama | 1051 |
|
Tallakshanaam | 1053 |
|
abbuda | 1056 |
|
nirabbuda | 1063 |
|
ahaha | 1070 |
|
ababa | 1077 |
|
atata | 1084 |
|
soganghika | 1091 |
|
uppala | 1098 |
|
kumuda | 10105 |
|
pundarika | 10112 |
|
paduma | 10119 |
|
kathana | 10126 |
|
mahakathana | 10133 |
|
asamkhyeya | 10140 |
|
dhvajagranishamani | 10421 |
Numbers above infinity
Below are some of the numbers representing Infinity
� bodhisattva (बोधिसत्व or बोधिसत्त) -1037218383881977644441306597687849648128
� lalitavistarautra (ललितातुलनातारासूत्र) -10200infinities
� matsya (मत्स्य) -10600infinities
kurma (कुरमा) -102000infinities
varaha (वरहा) -103600infinities
narasimha (नरसिम्हा) -104800infinities
vamana (वामन) -105800infinities
parashurama (परशुराम) -106000infinities
rama (राम) -106800infinities
khrishnaraja (कृष्णराज) -10infinities
kaiki (काईकी or काइकी) -108000infinities
balarama (बलराम) -109800infinities
dasavatara (दशावतारा) -1010000infinities
bhagavatapurana (भागवतपुराण) -1018000infinities
avatamsakasutra (अवताम्सकासुत्रा) -1030000infinities
mahadeva (महादेव) -1050000infinities
prajapati (प्रजापति) -1060000infinities
jyotiba (ज्योतिबा) -1080000infinities
Large number in other texts
Many ancient Indian texts talks about Lord Brahma being the creator of this universe and have often mention Lord Brahma to be trillions of years old. Below is the image extracted from such texts?
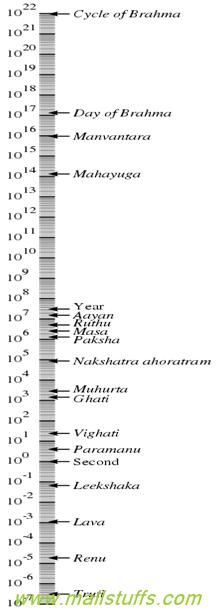
Hindu units of time in a logarithmic scale
When the world was thinking of one and two, Indian sages were dealing in trillions which is very evident in their religious thought. For example, in Vedas which is atleast ten thousand years old (as per carbon dating), we find Sanskrit words and verses corresponding to powers of 10 up to a trillion and even 1062. (Sanskrit words crores and lakhs, referring to 10,000,000 and 1,00,000 respectively, are in common use even today).
Large numbers in Surya Prajnapti
Another mathematical text Surya Prajnapti (wriiten around 400 BC) separates all numbers in three sets: enumerable, innumerable, and infinite. Each of these was further subdivided into three orders as:
• Infinite: nearly infinite, truly infinite, infinitely infinite
• Innumerable: nearly innumerable, truly innumerable and innumerably innumerable
Enumerable: lowest, intermediate and highest
Concept of Transfinite number
The concept of infinity is used in mathematical theory of limits. It is defined a number greater than any finite number. However, in the late 19th century, mathematicians started studying transfinite number. Transfinite number is a number which is not only greater than any finite number but also greater than infinity. Incidentally, it was the Indian mathematician ‘Jaina’ who first considered the concept of transfinite numbers in 400 BCE.
Large number in Taittiriya-Samhita
Taittiriya-Samhita written before 1000 B.C uses terminology for numbers up to order 10 ** 19 as
1, 10, 10**1, 10**2, 10**3, 10**4, 10**5, 10**6, 10**7, 10**8, 10**9, 10**10,
10**11, 10**12, 10**13, 10**14, 10**15, 10**16, 10**17, 10**18, 10**19.
However the terminology used in the medieval age varied slightly than those used in Taittiriya-Samhita. Also, as discussed above, the Valmiki Ramayana has specified the terminology for numbers up to the order of 10 **60. However, Point to be noted here is that term ‘samudra’ here denotes 10**9 whereas in the Taittiriya-Samhita, ‘Samudra’ represents 10**50 and many other terms for large numbers used by valmiki differs from those used in Tattriya-Samhita. Also, except this context, all other numerical terms used in valmiki Ramayana are same as those used in Taittiriya-Samhita e.g. Niyuta and Nyarbuda, Arbuda, Madhya, Antya, Samudra and Parardha. Probably, because of limited use of sequential large numbers, some of the numerical terms disappeared in the later literature and those which were found do not represent the same as used in ancient literature. For ex:
Samaranganasutradhara (11th century A.D.) uses padma for 10**13, , Sanku for 10 ** 12, Kharva for 10**10 and Vrnda for 10**9.
In the Taittiriya Upanishad, there is a section which signifies the quasi-mathematical relationship between the bliss of a Brahman (Enlightened individual) and the bliss of a young man who have all materialistic pleasure of this world. It says that a young handsome man who is fit, strong, healthy, and is the king of the world, is one unit of human bliss. Further, many human attributes are used to provide a series of multiplication to measure human bliss in 10010 units equal to spiritual enlightenment or salvation (Moksha).

Verses of Taittiriya-Samhita
Large numbers in Jainism
Jain scholars had a big fascination of large numbers. In fact, they were the first, scientific thinker to theorize that “all infinities are not the same or equal”. This idea was established in the modern world only in the late nineteenth century when Cantor initiated his theory of sets.
Beside concept of infinities, Jain scholars were also aware of indices related theory, though they did not used any convenient notation as we use in mathematics today. Instead of using notation, Jain used simple statements to specify theory of indices. Instead of calling square roots and squares, they used the term “first square root” or “second square” etc. For ex: consider the following statement from their texts: The first square root multiplied by the second square root is the cube of the second square root. According to what we learned about indices, this statement can be denoted
a1/2 x a1/4 = (a1/4 )3
Large numbers in Buddhism
Buddhist literature also describes finite, infinite, determinate and indeterminate numbers. Buddhist mathematicians classified mathematics as Garna (Simple Mathematics) or Sankhyan (Higher Mathematics). Numbers were of three types: Asankheya (uncountable), Sankheya (countable), and Anant (infinite).
According to Lalitavistara Sutra(a Buddhist work), there was a contest involving writing, arithmetic and archery, where buddha was defeated by great mathematician Arjuna who showed off his mathematical skills by citing the words representing numbers in power of ten up to 1 'tallakshana', equals to 1053. It also states that these words were just one of the series of counting system which geometrically expands up to 10421, that is, a 1 followed by 421 zeros.
The Decimal System in Harappa
No one knows the exact period of invention of number system and the modern world asks for proof of Vedas being millions of years old. So, let us go on the basis of evidences. As per the evidences, a decimal system existed during the pre-Harappa period. Archaeological evidences with weights corresponding to ratios of 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, and 500 have been found in Harappa and Mohenjo-Daro. However, the most notable characteristic of these weights and measures are their remarkable accuracy.
For Ex: A bronze rod marked with 0.367 inches exactly measures to .367 inches. Scales with unit of .367 inches were used in those days for proper planning and construction of towns, roads, drains, palaces, towers as per the guidelines laid out by the architect/King. This discovery of an accurate weight based system points to the existence of trade and commerce in the Harappa society.

Stones used as Weights during Harappa period
After the Harappa period, many Indian mathematicians introduced advanced concepts of place values system, integral calculus, differential equations etc which we will see in our next articles.
I will end this article with the following quotation from G.B. Halsted:
“The importance of the creation of the zero mark can never be exaggerated. This giving to airy nothing, not merely a local habitation and a name, a picture, a symbol, but helpful power, is the characteristic of the Hindu race from whence it sprang. It is like coining the Nirvana into dynamos. No single mathematical creation has been more potent for the general on-go of intelligence and power.”
Note: Images used on this website
are either a production of Bhaktivedanta Book Trust(https://www.krishna.com), Iskcon
Foundation or were found in google search under "Free to use and share". If any
of the images presented here violates copyright issues or infringes anyone copyright
or are not under "Fair use", then please bring it to our notice. Read
Disclaimer for more.
Share this to your friends. One of your friend is
waiting for your share.
Related Articles
Why cow is sacred to hindus
Common questions and myths of caste system
Science in Hinduism-Invention of numeral system
Ill effects of caste system
Why lord shiva is known as king of dance
Science in Hinduism-Place value and Decimal number system
Vedas Quotes Against Present Caste System
Why Dance worship in hinduism
Is god female-Yes or No
India most sacred river saraswati found
Post Comment